Método de Muskat para Predecir la Producción del Petróleo de un Yacimiento (Parte I)
Muskat considero el yacimiento como un medio poroso homogéneo a lo largo del cual la presión se mantiene uniforme. Muskat comparo esto con un tanque con válvulas de salida distribuidas continua y uniformemente utilizadas para drenar fluidos. Cada elemento de volumen del yacimiento produce a través de su propia salida y no existe intercambio de fluido entre los elementos de volumen. El comportamiento del yacimiento total se determinan a partir del comportamiento de cualquiera de los elementos de volumen que forman el yacimiento.
Este método se emplea en yacimientos de petróleo donde la producción se realiza mediante el empuje por gas en solución, el cuál puede incluir capa de gas e inyección de gas, así como a volúmenes de yacimientos que sean pequeños y su gradiente de presión sea despreciable. El comportamiento del yacimiento total se determina a partir del comportamiento de cualquiera de los elementos de volumen que forman el yacimiento.
Si So representa la saturación de petróleo a cualquier tiempo durante la producción del yacimiento; el volumen de petróleo a condiciones del yacimiento por barril de espacio poroso a condiciones normales vendrá dado como:
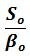
El volumen de gas viene expresado en pies cúbicos normales por barril a condiciones de yacimiento y está determinado por el gas en solución más el gas libre:

Los caudales de petróleo Qo y gas Qg a condiciones normales se expresan como el cambio del volumen de petróleo y gas existente en el espacio poroso, así pues:


Otra forma de ver la relación de gas petróleo instantánea Ri, es dividir el caudal de gas entre el caudal de petróleo, así:

Ahora bien si se expresa en función de la presión, siendo está la variable independiente, se puede reescribir como:

Así pues:

La Relación Gas Petróleo Instantánea Ri viene dada por:

Igualando las dos ecuaciones anteriores:

Despejando dSo/dP:

Donde:

Reemplazando los términos en la ecuación:

Esta es la ecuación que se conoce como la Ecuación de Predicción de Muskat en forma diferencial aplicada a yacimientos de empuje por gas en solución, la misma no posee solución analítica y por tanto debe resolverse numéricamente asumiendo decrementos finitos de presión, ΔP, quedando expresada como:

Con esta la ecuación se calcula directamente la variación de saturación para un cambio de presión específico. Los decrementos de presión deben ser pequeños con el fin de obtener una mejor oscilación numérica.
Los términos λ, σ y η son funciones de presión y se obtienen de las curvas de Rs, 1/ßg, y ßo en función de la presión. Para calcular el valor de ΔSo, correspondiente a un valor dado de ΔP = P1 - P2, los valores de λ, σ, η y μo/μg deben evaluarse a la presión promedia del intervalo, o sea, a (P1+P2)/2 ya que para intervalos pequeños de ΔP, puede asumirse una variación lineal entre P1 y P2 para un decremento de saturación ΔSo = ( So1 - So2 ). La determinación de kg/ko y ( 1 – So – Sw ) requiere del conocimiento de la saturación promedio correspondiente al decremento de presión dado o mediante el uso de correlaciónes empíricas como se efectúa en el presente trabajo. Este valor también podría determinarse por tanteo pero es demasiado arriesgado y poco recomendable. Si los decrementos de presión son pequeños puede, tomarse el valor de saturación de petróleo al comienzo del intervalo, es decir, el correspondiente a la presión P1, obteniéndose buenos resultados. Esto se hace normalmente en la práctica. Sin embargo es bueno tener presente que existe determinado error. Además los errores asociados son acumulativos y existe mayor error a medida que se toman decrementos mayores de presión. En otras palabras, es un método inestable.
Referencias:
- Universidad Central de Venezuela. Clases de Ingeniería de Yacimientos.
- Escobar, F. Fundamentos de Ingeniería de Yacimientos. Editorial: Universidad Surcolombiana. Bogota, Colombia, 2008.